Sometimes, it’s not easy to differentiate between squareness, perpendicularity, and parallelism. They are almost the same and have a close correlation. Even, squareness and perpendicularity are frequently used interchangeably while in fact, they are actually different.
On this great occasion, we are glad to present an article that covers the explanation of these terms.
Differences Among Squareness, Parallelism & Perpendicularity
Orientation Vs. Feature of Orientation
Parallelism and perpendicularity lie in a fundamental of GD&T (out of a total of four) known as orientation, while squareness is not commonly used in manufacturing and inspection but can be categorized as a feature of orientation. And all the orientation features require a datum; without a datum, these features cannot be controlled.
For example, if the orientation of a table is being measured, it would be measured in relation to a horizontal datum that would be the ground surface. In relationship to the floor, which we assume is level, in this case, the floor is acting as a “Datum Feature Simulator”, which in manufacturing is an equipment or a surface used to create a simulated datum.
The commonly used datum feature simulator in industries, manufacturing plants, and inspection units is the “Granite Surface Plate”, which is constructed by natural fine-grained granite and is smoothened afterward, leaving behind a very small value of flatness error. CMM machines also have a perfectly calibrated granite surface plate as their bed.
Other Aspects that Differ
The difference between these tolerances can also be stated in terms of their significance, condition for usage, procedure, how we measure them (different instruments to measure them) and symbols used to denote them.
The parallelism and perpendicularity could also be applied to axis but squareness can only be applied to surfaces. Another difference among the three could be their significance in usage. Among these three, squareness is the least important and thus least used because it can easily be defined using the combination of perpendicularity and parallelism.
Squareness
As the name suggests, the squareness is the property of a body being square. It determines the degree of how perfectly square a square object is.
Other than orientation control, squareness also requires symmetry with the opposite sides, otherwise, it cannot be categorized as a square. The squareness is not commonly used, but it is a significant tolerance feature.
There is a case that sometimes a square body can have accurate dimensions of length and width but is not yet considered a square. For instance, consider the following example of a 50 mm square.
It can be easily observed in this scenario that both length and width are correctly the same lengths but it is not a perfect square. Also, for squareness, the adjacent sides should be perfectly at 90 degrees to each other, which is not the case in the above-shown example.
Applications
Practically, many products are being used in everyday life requiring some certain value of squareness for proper assembly. For instance, some engine brackets may require squareness for proper assembly of them with other engine parts.
Unlike other tolerance types, the squareness does not have a proper symbol in GD&T, rather it is represented as a combination of parallelism, perpendicularity, and measure of diagonals.
Parallelism
On the other hand, parallelism determines how parallel two geometrical features/surfaces (that are supposed to be exactly parallel) to each other are.
If we extend both the surfaces/lines that are parallel, they will never intersect each other. If by any chance, they meet at some point, then it would mean that the geometrical features are angled toward each other.
Applications
In real-life applications, parallelism is used in manufacturing many important products, for instance, in the production of wheel hubs and brake drums. In both of these products, the right and left side of the outer diameter needs to be perfectly parallel. Otherwise, it would cause problems in assembly and during operation. A brake drum having sides not having parallelism up to a certain value may cause judder during operation.
Perpendicularity
On the contrary, perpendicularity determines the property of a geometrical surface/feature of being perpendicular to another surface. In other words, this feature is used where two geometrical features have a 90-degree angle between them. It’s also worth keeping in mind that the surfaces or lines should be straight. So, there are two straight surfaces/lines that are meeting at a certain point, shaping a 90-degree angle.
Applications
In real-life applications, tolerance of perpendicularity is critical in the manufacturing of products that need to sit on planar surface shoulders such as bolts, keys, and shafts.
The parallelism and perpendicularity are not only limited to the adjacent or opposing surfaces or planes but also applied to other geometrical features, including holes and pins. In these scenarios, perpendicularity and parallelism are applied on the axis of holes and pins.
Correlations Among Squareness, Parallelism & Perpendicularity
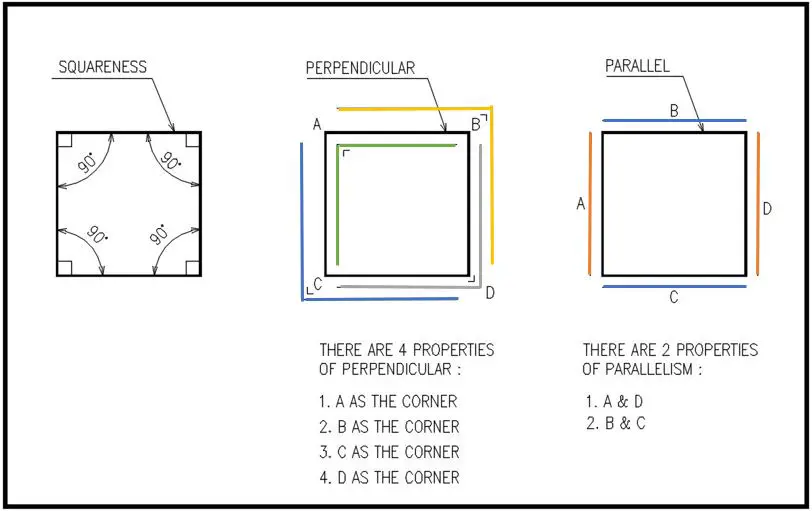
The squareness covers both the parallelism (for opposing sides/features) and perpendicularity (for adjacent sides/features) at the same time.
However, objects that have parallel opposite sides are not necessarily square. It may be a parallelogram.
A square object consists of several perpendicular lines/surfaces. That said, perpendicularity is a part of squareness.
Aside from that, the object surfaces should be flat or straight, be it for squareness, parallelism, and perpendicularity.
The tolerance zones for these 3 terms could be either parallel lines or planes.
Measurement of Squareness, Parallelism & Perpendicularity
All these three could be measured using modern technologies, including CMM, lasers, dial gauge indicator, digital height gauge, precision square, cylinder square, square tools, straight edge, feeler gauge, etc.
Measuring Squareness
Conventionally, for objects with not much accuracy is desired, a precision machinist square and a set of feeler gauges are used to measure the squareness of the object.
For this purpose, the object’s squareness to measure is placed on a granite surface plate and its sides are touched to the blade of a precision square. A feeler gauge is applied to check the gap that may exist on the 4 sides of that object. The feeler gauge functions to estimate the deviation.
Also, an accurate digital caliper is needed to measure the dimensions of both diagonals that need to be equal for the squareness of the body.
CMM is employed where high accuracy is desired. For measuring the dimensions of diagonals, the two edges are touched with the probe. It will verify the difference in measurement of both the diagonals whether it exceeds the maximum limit or not. Also, to check the 90-degree angle between the adjacent sides, the probe of CMM is touched on the sides of object and value of variation in the desired angle is obtained.
For more explanation about how to measure squareness, read more about it here.
Measuring Parallelism
Conventionally, parallelism is measurable using a height gauge with a dial indicator. The base of height gauge is placed on a granite surface plate along with the object whose parallelism is to be measured with its datum plane/surface on the surface plate.
As an alternative, you can replace the height gauge with a magnetic base.
Now, dial gauge is moved on the geometrical feature whose parallelism needs to be measured and the variation in parallelism of that surface is determined.
Using CMM, several points are taken on both surfaces that need to be measured and imaginary lines are drawn using CMM and angle between the two lines is determined and verified that it lies in the given range or within the desired tolerance zone.
Measuring Perpendicularity
Basically, measuring the perpendicularity is almost similar to measuring the squareness. Measuring the squareness assesses the 4 sides of the subject to measure while measuring the perpendicularity involves 2 sides only.
You could use a precision square with a feeler gauge to measure the gap. For better practice, you could use a more accurate instrument such as a dial indicator. In such a way, the dial indicator is clamped by a magnetic base stand that rests on a surface plate.
Perpendicularity can also be measured using CMM. Several points are taken on the feature whose perpendicularity needs to be measured along with several points on datum or granite surface plate. Using these points, imaginary lines are drawn. The angle between these lines are then obtained, and variation in the perpendicularity is then measured.
Low-cost perpendicularity measurement with lower accuracy can be performed with square tools such as try square, speed square, double square, combination square, etc. This case may happen frequently in the woodworking and carpentry projects.
Read also:
